Constructions en treillis

SOMMAIRE

A.Généralités

.Introduction

.Terminologie

A2.1. Poutres en treillis

A2.2. Les fermes

.Dispositions constructives

A3.1. Fermes traditionnelles et constructions soudées

A3.2. Comparaisons entre les assemblages soudés, mivés ou boulonnés.

B.Calcul des systèmes réticulés

.Introduction

.Définition

.Hypothèses de calcul

.Méthodes de calcul des efforts dans les systèmes triangulés

.But et moyens

.Méthode graphique : Cémona

.Méthode de culman

.Méthode manuelle : Ritter

.Calcul des ossatuves triangulées extérieurement hyperstatiques

.Exemples des ossatures

.Exemples de calcul

.Dimensionnement des barres

.Barres soumises à la traction

.Barres soumises à la compression

.Exemples

.Justification de goussets

.Principe de vérification

.Goussets sans flexion

.Goussets avec flexion

A - GENERALITES :

A1 - INTRODUCTION

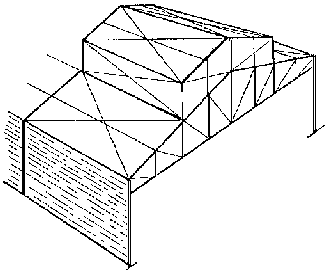
Les constructions métalliques, faites d'assemblages de profilés (L,T,I) par rivets, boulons, soudure, pour la construction de ponts, charpentes, grandes poutres, pylône, etc..., sont réalisées généralement avec des "systèmes triangulés" (éléments à treillis) fig. 1.

Alors que les éléments simples en profilés et les portiques travaillent en flexion, les éléments à treillis reprènenet les charges essentiellement par des efforts normaux : traction ou compression.

Bien que leurs formes ne soient pas idéales pour le flambement servent (voir RT n°) les cornières sont le plus souvent utilisées en raison des facilités qu'elles donnent pour les assemblages. Lorsque leurs sections deviennent insuffisantes, d'autres profilés U, I ou H peuvent être employés.

La généralisation de l'emploi de profilés, en général moins coûteux en main - d'oeuvre, a diminué le nombre des éléments en treillis. C'est ainsi que les poteaux et les pannes ne se font que rarement en treillis. Par contre, les fermes en treillis restent plus économiques, d'autant que leur exécution est devenue moins onéreuse avec le banc de perçage, les machines de production et de perçage des goussets... Elles ont l'avantage d'assurer l'encastrement des poteaux avec une inertie plus importante que celle d'une traverse de portique.

Elles subsistent donc lorsque l'esthétique est sans importance, lorsque le dégagement de l'espace du comble n'est pas utile ou encore si un plafond est prévu au niveau des entraits. D'autres éléments sont également prévus en treillis : les contreventements notamment en toiture, les pylônes etc...

Bâtiment en Treillis

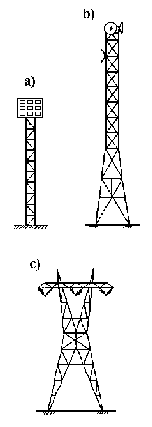
Pylônes électriques

Fig - 1- Exemples d'éléments à Treillis

A2 - Terminologie :

A2-1 - Poutres en treillis :

Dans ce genre de poutres, l'âme est remplacée par un système de triangulation à base de plats, cornières, tès, tubes etc...

La partie supérieure, formant l'encadrement, se nomme membrure supérieure ou extrados, et la partie inférieure se nomme membrure inférieure ou intrados.

On notera que les membrures peuvent être parallèles cas des poutres à inertie constante, en queue de billard ou galbée symétrique ou non, cas des poutres à inertie variable.

L'ensemble de la triangulation formant les membres est appelé étrésillon, les éléments verticaux prennent le nom de montants et les parties inclinées celui de diagonales.

On distingue différentes formes de poutres :

• Poutres en N dites de Pratt ou de Howe :

• Poutres en V dites de VARREN

• Poutre en X dites en croix de St André :

• Poutre en K :

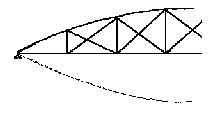
• Poutres paraboliques dites de Bow-String :

• Poutre Schwedler :

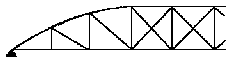
A2-2 - Les fermes :

Les fermes sont les poutres maîtresses d'un toiture. Elles sont constitués le plus souvent par un système triangulé. Généralement les barres sont composées de deux cornières disposées symétriquement par rapport au plan de la ferme. Dans certains cas, les cornières sont mises en croix (aile de moulin) pour des raisons de symétrie ou d'entretien, mais souvent les corniers sont jumelées.

Terminologie d'une ferme :

On remarquera que la membrure inférieure peut être droite ou relevée. On distingue plusieurs formes de fermes :

• Forme anglaise :

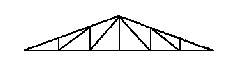
• Forme américaines :

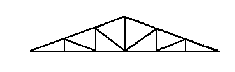
Le choix d'une ferme doit tenir compte des facteurs suivants :

• Type de couverture (espacement des pannes, pentes admissibles, ...),

• Portée des fermes,

• Conditions particulière (architecture, entretien, ...),

L'écartement des fermes peut varier dans les limites très larges.

Un petit écartement conduit à un nombre élevé des fermes et par lie un excès de poids. Par contre les pannes deviennent légères.

Un grand écartement amène une construction économique des fermes et une utilisation optimale de matériaux mais les pannes deviennent lourdes.

Il faut donc étudier le problème de fermes - pannes simultanément.

L'écartement des fermes pour de bâtiments à toitures légères varie entre 4 et 6 m.

A3 - Dispositions constructives :

A3.1- Fermes traditionnelles et fermes en Constructions soudées :

Les membres et les étrésillons sont généralement prévues en cornières simples ou doubles. On peut avoir deux types de constructions en treillis : construction assemblés par l'intermé-diaire de gousset et constructions soudés.

a - Assemblage par goussets :

Les goussets sont assez fréquemment des points de la construction réticulée (poutre et ferme treillis etc...), car ils travaillent dans des conditions défavorables aux points où les membrures (arbalétriers et entraits) sont interrompues et même diviées. Toutefois, on peut avoir quelques recommandations.

• Au niveau du faîtage, les cornières arbeletries sont coupés droits ou d'onglet avec un intervalle minimal (fig. ...).

Les attaches sur poteaux sont soumises généralement à des efforts verticaux dus aux charges horizontaux résultants de l'encastrement des fermes qui sont prépondérantes, le centrage de l'épure sur le nu intérieur de poteau à l'avantage de solliciter les boulons d'attache au cisaillement pur, sans être gênant pour les poteaux. (fig. ...)

Lorsque les effort d'encastrement sont importants, il est plus avantageux de centrer l'épure à l'intérieur du poteau dans le cas de goussets séparés pour l'arbalétrier et l'entrait (fig. ...).

Ferme belge : Ferme polonceau : Ferme à la Mancard :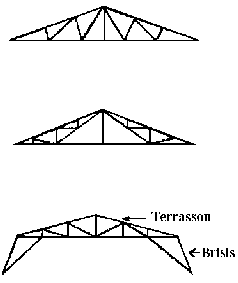

Ferme cartilever : Ferme en parpluies : Shed :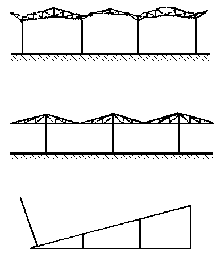

Exemple d'assemblage par goussets :

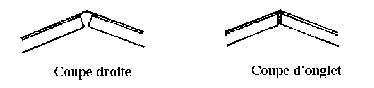
Fig. ...

Fig. ... Fig. ...

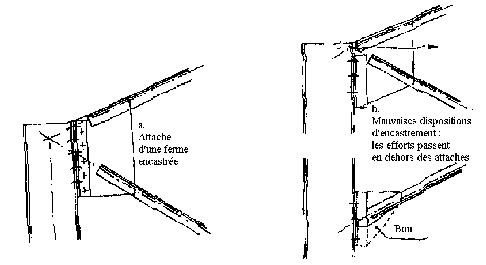
Fig. ...

On distingue les goussets verticaux assurant seuls le rôle des joints et d'autres qui jouent le rôle de couvre joints des membrures. (fig. ...)

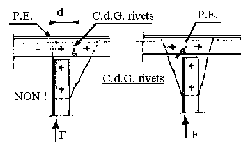
Pour éviter les problèmes, des règles sont applicables aux goussets :

• Le gousset doit, par sa forme et par la disposition de l'assemblage, éviter (ou réduire au minimum) l'excentricité des efforts par rapport aux sections du gousset qui sont principalement sollicitées. (fig. ...)

• Pour joint des membrures principales, on doit prévoir des couvres-joints sans tenir compte de gousset.

• On ne doit jamais donner aux goussets des angles rentrants ou dans le vide.

• On doit donner aux goussets une forme aussi régulière que possible, ayant au moins deux bords perpendiculaires ou parallèles.

Conception des goussets :

1- Réduire les dimensions :

2- Forme idéale : le rectangle (s'en approche autant que possible) :

3 - Réduire le nombre de coupes et chutes :

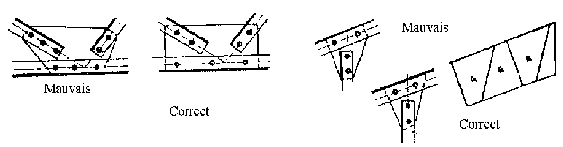
• Au moins 2 côtes parallèles,

• Autant que possible couper à angles droits,

• Côtes rondes pour utiliser bondes de tôles.

4 - Eviter les angles rentrants :

5 - Pas de coins de gousset dans le vide :

6 - Trous dissymétriques pour éviter les erreurs au montage :

7 - Les fourrures doivent toujours être fixées a part sur le gousset :

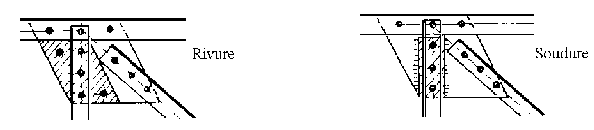
b - Assemblages :

• Conception générale :

En dehors des dispositions courantes on utilise encore pour les fermes de grandes portée le système caisson où les membres sont en U et les étrésillons en cornières jumelées par les traverses de liaison. (fig. ...).

Poutre soudée «en caisson»

Fig. ...

Les deux écueils suivants doivent être évités.

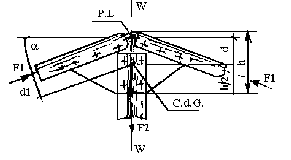
• L'insuffisance de sections de l'âme de la membrane : celle-ci est sollicitée par l'effort longitudinal et l'effort tranchant transversal, dont la combinaison est particulièrement dangereuse au voisinage des extrémités de la ferme encastrés sur les poteaux. On y remédie par l'élargissement de l'âme au moyen d'un gousset. (fig. ...)

• La trop grande raideur des treillis : les fermes sont calculées comme des systèmes réticulés à l'articulation parfaites. Or les barres sont encastrés les unes sur les autres aux noeuds et leurs déformations modifiant les angles de leurs épures ont pour effet d'entraîner leur flexion. La construction soudée a moins de ressources d'adaptation que la construction boulonnée ou rivée. ( fissuration au niveau de la soudure). On peut éviter cet inconvénient sur découpant la membrane suivant une couche d'assez grand rayon et en démontant la soudure du gousset.

Sur la partie droite de l'élargissement. (fig. ...)

Fig. ...

• Il ne faut pas oublier «d'équilibrer» les soudures des barres treillis :

Le centre de gravité des cordons doit en principe coïncider avec le fibre neutre de la barre attachéé. (fig. ...)

• Faîtage et rentrants :

Si les joints de montage se trouvent en ces points, ils sont établis comme il a été indiqué précédemment.

Dans le cas où les angles sont à assembler en atelier, les changements de direction des ailes des membranes doivent être soutenus par des raidisseurs soudés à la fois sur le plis et sur l'âme. (fig. ...)

• Attaches sur poteau :

Elles se font généralement par platine d'épaisseur suffisante pour ne pas fléchir sous les efforts de traction appliquée au boulons, qui peuvent être complétées par un couvre joint entre semelle de membre supérieure et le poteau. (fig. ...)

Les encastrement soumis à des moments importants sont traités comme ceux des portiques par soudure au chantier. (fig. ...)

Fig. ... Fig. ...

A3.2 - Comparaison entre les assemblages soudés et les assemblages rivés ou

boulonnés :

Dans la conception d'un assemblage on doit tenir compte des caractéristiques d'un moyen d'assemblage adopté.

• On doit choisir la forme logiquement la plus indiquée qui découle du mode de transmission des efforts par les organes de liaison (soudures, rivures ou boulons). Il en résulte que les assemblages soudés permettent plus de liberté que les assemblages rivtés ou boulonnés dans la position, l'une par rapport à l'autre, des pièces à assembler.

• Il faut également adopter les dispositions nécessaires pour assurer la même sécurité pour toutes les sections de rupture possible. Il en résulte pour un même assemblage des solutions entièrement différentes en soudé et en rivé ou boulonné.

• L'exécution dans de bonnes conditions d'un assemblage soudé nécessite un personnel rigoureusement spécialisé, car la qualité, et donc la résistance de cette catégorie d'assemblages dépend beaucoup de l'exécution. Les défauts étant moins décelables qu'en rivtés ou boulonnés.

• Les assemblages soudés sont dans leur nature, plus rigide que les assemblages visés ou bolonnés, qui permettent ce meilleure adaptation.

B - Calcul des systèmes réticulés :

B1 - Introduction :

B1.1 - Définition :

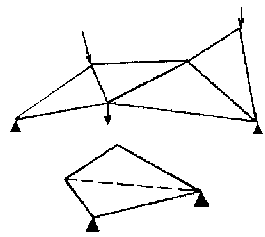
Systèmes plans, composés de barres rectilignes indéformables, obtenus en juxtaposant des triangles (le triangle étant la figure indéformable la plus simple).

Il existe une relation entre le nombre de barre b et le nombre de noeuds  dans un système triangulé.

Système indéformable : b = 2n - 3 b = 9 n = 6 Système déformable : b < 2n - 3 b = 4 et n = 4 On peut le rendre indéformable en ajoutant une diagonale. Système surabondant : ou système hyper-statique inférieurement dans ce cas : b = 2 n b = 8 et n = 5

B1-2 - Hypothèses de calcul :

Dans la suite on n'envisage que des systèmes indéformables, on supposera toujours que le forces extérieures ne sont appliqués qu'aux noeuds.

On suppose que les noeuds sont parfaitement articulés ce qui n'est pas le cas, en effet on réalise souvent des liaisons par rivtés, boulons, ou soudure, ce qui donne dans la plupart des cas un véritable encastrement.

Il en résulte des efforts supplémentaires que l'on désigne par effets secondaires.

Le calcul des efforts secondaires est très complexe même dans les cas qui paraissent les plus simples.

Pour les systèmes réticulés sans encastrement, on peut se dispenser de calculer les efforts secondaires si est de l'ordre de 0,2 à 0,3 cm3.

avec I : Montant d'inertie de la barre (cm4).

I : Longueur de la barre (cm).

B2 - Méthode de calcul des efforts dans des systèmes triangulés :

B2.1 - But et Moyens :

On se propose de calculer l'effort (de traction ou de compression) supporté par chacune des barres, en fonction des charges appliquées à la construction étudiée.

La méthode de calcul des systèmes est basée sur l'étude de l'équilibre d'une barre et d'un noeud.

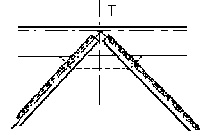
Soit une barre soumise à deux forces : A et B.

Pour qu'elle soit en équilibre, les deux forces doivent être égales et directement opposées.

Si A et B tendent à éloigner leurs points d'application respectifs, la barre est tendue.(fig. ...) Dans le cas contraire, elle est comprimée. (fig. ...)

Fig. ... Fig. ...

Réciproquement, une barre ne peut agir sur un noeud considéré auquel elle aboutit, que suivant sa droite d'action AB. Si la barre est tendue, elle tirera sur le noeud avec la même intensité que le noeud tire sur elle.

Si elle est comprimée, elle poussera sur le noeud.

Pour l'équilibre d'un noeud, on cherchera la résultante en B des forces connues (fig. ...) et on en déduira les actions inconnue, à condition qu'elles se réduisent à deux.

Pour le calcul de ces efforts, il existe plusieurs méthodes qui sont :

• Méthode graphique dite de Crémoma.

• Méthode dite de Culman.

• Méthode dite de Ritter.

B2.2 - Méthode de Crémona :

En étudie de poche en poche l'équilibre des différents noeuds, en partant généralement d'une extrémité d'une construction en treillis.

• Etapes de la méthodes :

• On adopte un sens pour passer d'un noeud aux suivants (nous adapterons le sens des aiguilles d'une montre).

• Il faut au préalable connaître toutes les forces extérieures appliquées à l'ouvrage étudié, donc détrerminer graphiquement ou par le calcul les réactions aux appuis.

• On appelle CREMONA la juxtaposition ordonnée des polygon des forces relatifs aux différents noeuds, en vue de simplifier l'épure.

• On ne trace pas de polygone funiculaire, sauf pour déterminer les réactions de contact aux appuis.

• Chaque fois que l'on passe d'un noeud au suivant, il ne faut pas perdre de vue que l'action d'une barre sur un noeud est égale et directement opposée à l'action de cette barre sur le noeud précédent (équilibre de la barre).

• A chaque noeud on ne doit avoir que deux forces inconnues.

• Si en un noeud on est en présence de tension inconnues dans trois barres, le problème est «hyperstatique» : il faut recourir à une autre méthode ou se demander s'il n'y a pas une barre surabondante.

• Si en un noeud il n'y a qu'une tension de barre inconnue, la fermeture du polygone des force, relative à ce noeud, sert de contrôle, car la résultante des forces connues doit être dirigée suivant la direction de la barre dont on cherche la tension.

• Si l'ouvrage est symétrique (c'est le cas de beaucoup de charpentes) par rapport à un plan vertical par exemple, avec des charges ayant le même plan de symétrie, il est suffisant, en général, d'en étudier la moitié (V.problèmes).

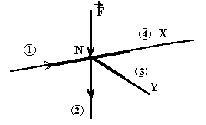
Exemple : voir fig. - Etude d'un noeud N.

F : force appliquée (charge verticale) (1) : action de la barre  sur N, (barre comprimée), donc action dirigée vers N.

(2) : action de la barre  sur N (barre tendue). donc action dirigée de N vers 2. On cherche : X - action de la barre 4 sur N Y - action de la barre 3 sur N 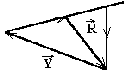Fig. ... On part d'un point quelconque A, d'où : (1) + (2) + F + X +Y = 0 (on termine au point A) (R : résultante)

Jusqu'à maintenant, nous avons numéroté les barres (1,2,...) et avons adopté les numéros correspondants sur l'épure de Crémona. Cette façon de faire est utilisée.

Cependant, il existe une autre méthode de repérage, qui semble préférable, notamment dans le cas où le Crémona est complexe avec plusieurs vecteurs sur le même support. En voici brièvement le principe.

• Chaque région délimitée par trois barres est repéré par un chiffre (1,2,...).

• Chaque région délimitée par deux forces est réparée par une lettre minuscule (a, b, ...).

Dans ce cas chaque force est désignée par les deux lettres correspondant aux régions qu'elles divise.

• On commence par tracer le dynamique des forces extérieures, puis après les autres forces dans les barres.

Voir la marche à suivre dans la page suivante.

Tracé de Crémona

Marche à suivre

1. Dessin du schéma de triangulation (choix de l'échelle)

2. Implantation des charges aux noeuds du système (forces extérieures) (les charges

n'attaquent qu'on droit des noeuds).

3. Calcul et implantation des réactions d'appuis (forces extérieures).

4. Numérotation, des surfaces interceptées par les barres (forces intérieures). Les charges et

les réactions d'appuis (forces extérieures).

5. Tracé du dynamique :

a - Choix de l'échelle des forces

b - Sens de rotation autour des noeuds (suivant les aiguilles d'une montre)

c - On commence par les forces connues pour tracer le polygone dynamique, en

tournant dans le sens adopté).

6. Le sens de parcours (cheminement) de chaque polygone des forces détermine la direction

des efforts recherchés sur le tracé.

7. Sur le schéma de triangulation, porter les flèches au noeud correspondant du polygone

des forces.

8. Les sens des flèches indique la nature des efforts.

9. Dresser un tableau des efforts .

10. Sur le schéma d'épure, renforcer les barres comprimées.

Exemple : Soit une ferme polonceau de 12m de portée (fig. ...), soumis à trois charges égales à P et deux charges égales à P/Z, appuyée directement sur deux murs : A : appui rotule et B : appui simple. P = 100 daN.

L'équilibre donne : RA + RB 

Chaque force extérieure divise le plan en deux régions repérées par des lettres a, b, c, ...

Chaque force relative à une barre (force intérieure) divise le plan en deux zones repérées par des numéros : 1, 2, 3, ...

• Tracé du dynamique : Ech : 1 cm = 400 daN.

On va commencer le tracé à partir du noeud A. On trace d'abord le polygone des efforts extérieurs, puis on doit chaque noeud, fermer le polygone des forces.

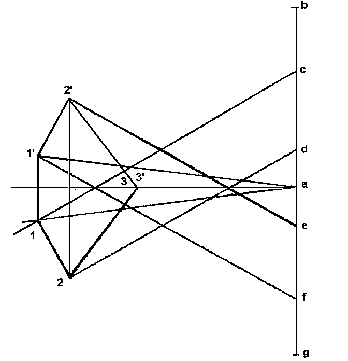
• Tableau des efforts :

Barres al cl d2 12 a3 23 + : Traction

Effets (daN) +3400 -3880 -3400 -840 +2080 +1440 - : Compression

Les efforts dans les autres barres sont symétriques.